Kužeľosečky

Príklad 1

Rozhodnite, či nasledujúca rovnica je analytickým vyjadrením elipsy
$$9x^2+25y^2-54x-100y-44=0.$$

Riešenie

Upravíme

$$\begin{array}{lcr} 9x^2+25y^2-54x-100y-44&=&0\\ 9(x^2-6x)+25(y^2-4y)&=&44\\ 9[(x-3)^2-9]+25[(y-2)^2-4]&=&44\\ 9(x-3)^2-81+25(y-2)^2-100&=&44\\ 9(x-3)^2+25(y-2)^2&=&225\\ \frac{(x-3)^2}{25}+\frac{(y-2)^2}{9}&=&1 \end{array}$$

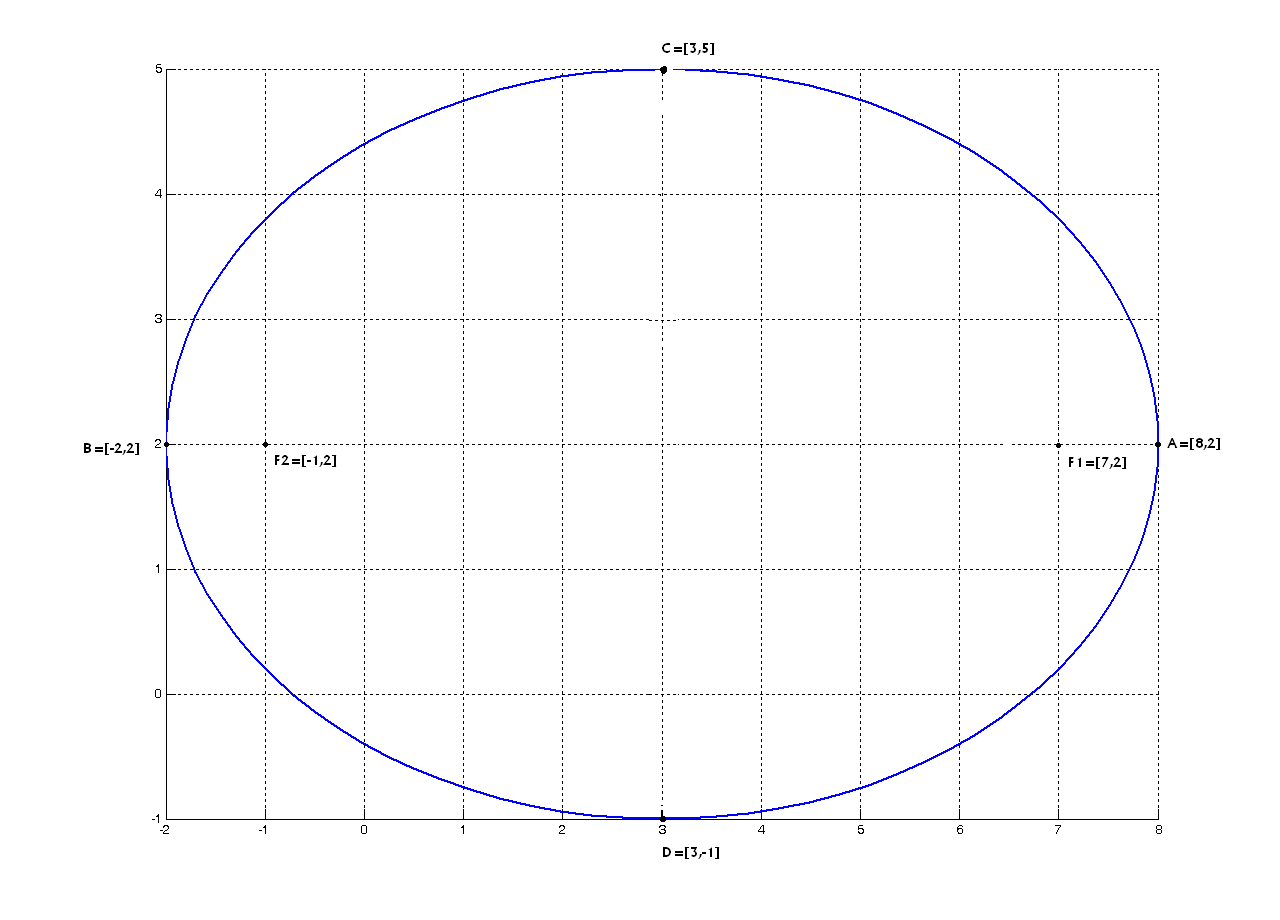
Rovnica  $$\frac{(x-3)^2}{25}+\frac{(y-2)^2}{9}=1$$ je stredová rovnica elipsy so stredom v bode $S=[3,2]$, dĺžkou hlavnej poloosi $a=5$, dĺžkou vedľajšej poloosi $b=3$ a excentricitou $e^2=a^2-b^2$, t.j. $e=4$.

Často sa k popisu elipsy uvádzajú aj súradnice významných bodov kužeľosečky. Pri elipse sú to

• súradnice ohnísk sú $F_1=[3+4,2]$ a $F_2=[3-4,2]$, t.j. $F_1=[7,2]$ a $F_2=[-1,2]$,
• súradnice hlavných vrcholov elipsy sú $A=[3+5,2]$ a $B=[3-5,2]$, t.j. $A=[8,2]$ a $B=[-2,2]$,
• súradnice  vedľajších vrcholov elipsy sú $C=[3,2+3]$ a $D=[3,2-3]$, t.j. $C=[3,5]$ a $D=[3,-1]$.

Súčasťou riešenia je náčrt samotnej elipsy.